10 Apr 2016
1. Basics
Hadoop ecosystem:
- HDFS: a distributed file-system for Hadoop
- HBase: Hadoop NoSQL database
- Hive: Hadoop data warehouse
- Pig: Data analysis high-level language
- Storm: Distributed real-time computation system
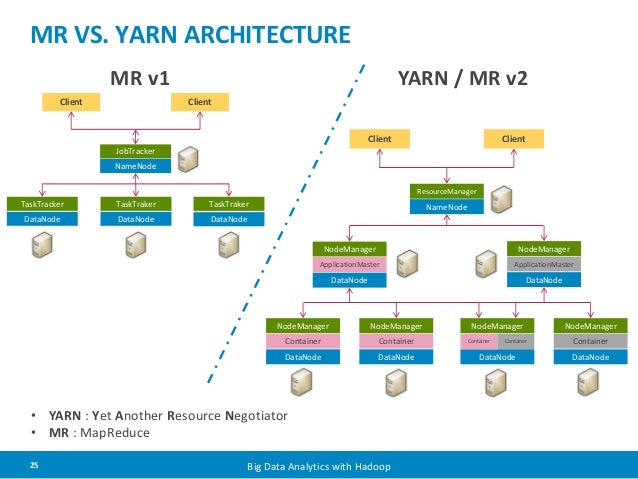
- Yarn: a resource-management platform responsible for managing computing resources in clusters and using them for scheduling of users’ applications.
- MapReduce: a programming model for large scale data processing.
- ZookKeeper: Hadoop centralized configuration system
HDFS:
- Highly scalable
- Support parallel reading and processing of the data
- Fault toleratn and easy management
MapReduce: A MapReduce job splits a large data set into independent chunks and organizes them into key, value pairs for parallel processing.
- The Map function divides the input into ranges by the InputFormat and creates a map task for each range in the input.
map(key, value) -> list<key2, value2>
- The Reduce function then collects the various results and combines them to answer the larger problem that the master node needs to solve.
reduce(key2, list<value2>) -> list<value3>
YARN (Yet Another Resource Negotiator): split up two major responsibilities of JobTracker(the resource management and job scheduling/monitoring) into separate daemons: a global Resource Manger and per-application Application Master.
Hive: a SQL like query language to run queries on large volumes of data for ETL.
- Not for online transaction processing
- Not for real-time queries and low-level updates
- Ad-hoc queries, summarization, and data analysis
Pig: provide rich data structures and make transformations much easier. It translates the Pig Latin script into MapReduce.
- for ETL (Extract -> Transform -> Load)
- for preparing data for easier analysis
- for long series of data operations
Tez: is an extensible framework for building high performance batch and interactive data processing applications, coordinated by YARN in Apache Hadoop.
Tutorials:
I followed this tutorial to install the sandbox for Hortonworks Data Platform.
After start the sandbox, we can open a webpage with 127.0.0.1:8888, and get

Then, we can login the sandbox with:
# ssh <username>@<hostname> -p <port>
ssh root@127.0.0.1 -p 2222;
We can also explore the Ambari page, which is like an adimn system aimed at making Hadoop management simpler. The Ambari page is like this

Update Ambari password: $ ambari-admin-password-reset
Here is the word count example implemented as a MapReduce program using the framework:
# Part 1
mr = MapReduce.MapReduce()
# Part 2
def mapper(record):
# key: document identifier
# value: document contents
key = record[0]
value = record[1]
words = value.split()
for w in words:
mr.emit_intermediate(w, 1)
# Part 3
def reducer(key, list_of_values):
# key: word
# value: list of occurrence counts
total = 0
for v in list_of_values:
total += v
mr.emit((key, total))
# Part 4
inputdata = open(sys.argv[1])
mr.execute(inputdata, mapper, reducer)
2. Hive
# simple code for creating a table
hive > CREATE TABLE mytable (name string, age int)
ROW FORMAT DELIMITED
FIELDS TERMINATED BY ';'
STORED AS TEXTEFILE;
# for load data
hive > LOAD DATA LOCAL INPATH
'data.csv' OVERWRITE INTO
TABLE mytable;
# insert data
hive > INSERT INTO birthdays SELECT
firstName, lastName, birthday FROM
customers WHERE birthday IS NOT NULL;
# create a table and insert data into it
hive > CREATE TABLE age_count (name string, age int);
hive > INSERT OVERWRITE TABLE age_count
SELECT age, COUNT(age)
FROM mytable;
Hive supports subqueries only in the FROM clause
hive > SELECT total FROM (SELECT c1 + c2 AS total FROM mytable) my_query;
Common operations:
- See current tables:
hive> SHOW TABLES;
- Check the schema:
hive> DESCRIBE mytable;
- Check the table name:
hive> ALTER TABLE mytable RENAME to mt;
- Add a column:
hive> ALTER TABLE mytable ADD COLUMNS (mycol STRING);
- Drop a partition:
hive> ALTER TABLE mytable DROP PARTITION (age=17);
Load data:
LOAD DATA INPATH '/tmp/trucks.csv' OVERWRITE INTO TABLE trucks_stage;
The file trcuks.csv is moved to /apps/hive/warehouse/truck_stage folder.
ORC(Optimized Row Columnar) file format provides a highly efficient way to sotre Hive data. Create an ORC table: CREATE TABLE ... STORED AS ORC ...
To use Hive command lines:
$ su hive
$ hive
# To quit
$ quit
- Use STORED AS TEXTFILE if the data needs to be stored as plain text files.
- Use STORED AS SEQUENCEFILE if the data needs to be compressed.
- Use STORED AS ORC if the data needs to be stored in ORC file format.
- Use ROW FORMAT SERDE for the RegEx SerDe.
- Use INPUTFORMAT and OUTPUTFORMAT in the file_format to specify the name of a corresponding InputFormat and OutputFormat class as a string literal.
Partitioned tables can be created using the PARTITIONED BY clause. A table can have one or more partition columns and a separate data directory is created for each distinct value combination in the partition columns.
The EXTERNAL keyword lets you create a table and provide a LOCATION so that Hive does not use a default location for this table.
Tables can also be created and populated by the results of a query in one create-table-as-select (CTAS) statement.
CREATE TABLE new_key_value_store
ROW FORMAT SERDE "org.apache.hadoop.hive.serde2.columnar.ColumnarSerDe"
STORED AS RCFile
AS
SELECT (key % 1024) new_key, concat(key, value) key_value_pair
FROM key_value_store
SORT BY new_key, key_value_pair;
The LIKE form of CREATE TABLE allows you to copy an existing table definition exactly (without copying its data).
CREATE TABLE empty_key_value_store
LIKE key_value_store;
3. Pig
Pig Latin allows you to write a data flow that describes how data will be transformed (such as aggregate, join and sort). It can be extended using other languages such as Java and Python.
Pig data types:
- Tuple: ordered set of values
- Bag: unordered collection of tuples
- Map: collection of key value pairs
# Example
logevents = LOAD 'my.log' AS (date: chararray, level: chararray, code: int, message: chararray);
severe = FILTER logevents BY (level == 'severe' AND code >= 500);
grouped = GROUP severe BY code;
STORE grouped INTO 'severevents';
Debugging tips:
- Use
illustate, explain, and describe
- Use local mode to test script before running it in the cluster
Examples:
// load data from a file names geolocationusing HCatLoader()
a = LOAD 'geolocation' USING org.apache.hive.hcatalog.pig.HCatLoader();
// filter dataset
b = FILTER a BY event != 'normal';
// iterate through all the records
c = FOREACH b GENERATE driverid, event, (int) '1' AS occurance;
// group by driver id and iterate over each row
d = GROUP c BY driverid;
// add to the occurance
e = FOREACH d GENERATE GROUP AS driverid, SUM(c.occurance) AS t_occ;
g = LOAD 'drivermileage' USING org.apache.hive.hcatalog.pig.HCatLoader();
h = JION e BY driverid, g BY driverid;
final_data = FOREACH h GENERATE $0 AS driverid, $1 AS events, $3 AS totmiles, (float) $3/$1 AS riskfactor;
STORE final_data INTO 'riskfactor' USING org.apache.hive.hcatalog.pig.HCatStorer();
Example from Hortonworks : Transfrom NYSE data
\\ Define a relation with a schema
STOCK_A = LOAD '/user/maria_dev/NYSE_daily_prices_A.csv' USING PigStorage(',')
AS (exchange:chararray, symbol:chararray, date:chararray,
open:float, high:float, low:float, close:float, volume:int, adj_close:float);
DESCRIBE STOCK_A;
\\ Defien a new relation based on existing one
B = LIMIT STOCK_A 100;
DESCRIBE B;
\\ View data relation
DUMP B;
\\ Select specific columns
C = FOREACH B GENERATE symbol, date, close;
DESCRIBE C;
\\ Store relationship data into a HDFS file
STORE C INTO 'output/C' USING PigStorage(',');
\\ Perform a join
DIV_A = LOAD 'NYSE_dividends_A.csv' using PigStorage(',')
AS (exchange:chararray, symbol:chararray, date:chararray, dividend:float);
D = JOIN STOCK_A BY (symbol, date), DIV_A BY (symbol, date);
DESCRIBE D;
\\ Order By
E = ORDER DIV_A BY symbol, date asc;
\\ Group By
F = FILTER DIV_A BY symbol=='AZZ';
G = GROUP F BY dividend;
Nulls and Load Functions:
A = LOAD 'student' AS (name, age, gpa);
B = FILTER A BY name is not null;
A = LOAD 'data' USING MyStorage() AS (T: tuple(name:chararray, age: int));
B = FILTER A BY T == ('john', 25);
D = FOREACH B GENERATE T.name, [25#5.6], {(1, 5, 18)};
A = LOAD 'data' AS (f1:int, f2:int, B:bag{T:tuple(t1:int,t2:int)});
DUMP A;
(10,1,{(2,3),(4,6)})
(10,3,{(2,3),(4,6)})
(10,6,{(2,3),(4,6),(5,7)})
X = FOREACH A GENERATE f2, (f2==1?1:COUNT(B));
DUMP X;
(1,1L)
(3,2L)
(6,3L)
A = LOAD 'data' AS (f1:int, f2:int,f3:int);
DUMP A;
(1,2,3)
(4,2,1)
(8,3,4)
(4,3,3)
(7,2,5)
(8,4,3)
B = GROUP A BY f1;
DUMP B;
(1,{(1,2,3)})
(4,{(4,2,1),(4,3,3)})
(7,{(7,2,5)})
(8,{(8,3,4),(8,4,3)})
Hive and Pig Data Model Differences:
- Pig: All data objects exist and operated on in scirpt. Once the script is complete all data objects are deleted unless you stored them.
- Hive: Operate on Hadoop data store. Data, tables, and queires persist from query to query. All data is live compared to Pig.
4. MapReduce
mrjob is the easiest route to writing Python programs that run on Hadoop. If you use mrjob, you’ll be able to test your code locally without installing Hadoop or run it on a cluster of your choice.
# Word Count example
from mrjob.job import MRJob
class MRWordFrequencyCount(MRJob):
def mapper(self, _, line):
words = line.split()
for word in words:
word = unicode(word, "utf-8", errors="ignore")
yield word.lower(), 1
def reducer(self, key, values):
yield key, sum(values)
if __name__ == '__main__':
MRWordFrequencyCount.run()
# Use MRStep to do multi-step
from mrjob.job import MRJob
from mrjob.step import MRStep
import re
WORD_REGEXP = re.compile(r"[\w']+")
class MRWordFrequencyCount(MRJob):
def steps(self):
return [
MRStep(mapper=self.mapper_get_words,
reducer=self.reducer_count_words),
MRStep(mapper=self.mapper_make_counts_key,
reducer = self.reducer_output_words)
]
def mapper_get_words(self, _, line):
words = WORD_REGEXP.findall(line)
for word in words:
word = unicode(word, "utf-8", errors="ignore") #avoids issues in mrjob 5.0
yield word.lower(), 1
def reducer_count_words(self, word, values):
yield word, sum(values)
def mapper_make_counts_key(self, word, count):
yield '%04d'%int(count), word
def reducer_output_words(self, count, words):
for word in words:
yield count, word
if __name__ == '__main__':
MRWordFrequencyCount.run()
- The
mapper() method takes a key and a value as args and yields as many key-value pairs as it likes.
- A
combiner takes a key and a subset of the values for that key as input and returns zero or more (key, value) pairs.
- The
reduce() method takes a key and an iterator of values and also yields as many key-value pairs as it likes.
You can use -r inline (the default), -r local, -r hadoop, or -r emr.
5. Spark
Apache Spark was designed to be a fast, general-purpose, easy-to-use computing platform. It extends the MapReduce model and takes it to a whole other level. The speed comes from the in-memory computations. Applications running in memory allow for much faster processing and response.
Zeppellin is a web-based notebook that enables interactive data analytics. It’s like Ipython Notebook.
Spark’s primary core abstraction is called a Resilient Distributed Dataset or RDD. It is a distributed collection of elements that is parallelized across the cluster. In other words, a RDD is an immutable collection of objects that is partitioned and distributed across multiple physical nodes of a YARN cluster and that can be operated in parallel.
SparkContext is the main entry point to everything Spark. It can be used to create RDDs and shared variables on the cluster.
\\ spark code for risk factor analysis
\\ import sql libraries
import org.apache.spark.sql.hive.orc._
import org.apache.spark.sql._
\\ instantiate HiveContext
val hiveContext = new org.apache.spark.sql.hive.HiveContext(sc)
\\ view list of table in Hive Warehouse
hiveContext.sql("show tables").collect.foreach(println)
\\ query tables to build spark RDD
val geolocation_temp1 = hiveContext.sql("select * from geolocation")
val drivermileage_temp1 = hiveContext.sql("select * from drivermileage")
\\ register a temporary table
geolocation_temp1.registerTempTable("geolocation_temp1")
drivermileage_temp1.registerTempTable("drivermileage_temp1")
\\ perform an iteration and a filter operation
val geolocation_temp2 = hiveContext.sql("SELECT driverid, count(driverid) occurance from geolocation_temp1 where event!='normal' group by driverid")
geolocation_temp2.registerTempTable("geolocation_temp2")
geolocation_temp2.collect.foreach(println)
val joined = hiveContext.sql("select a.driverid,a.occurance,b.totmiles from geolocation_temp2 a,drivermileage_temp1 b where a.driverid=b.driverid")
joined.registerTempTable("joined")
\\ view the results
joined.collect.foreach(println)
val risk_factor_spark=hiveContext.sql("select driverid, occurance, totmiles, totmiles/occurance riskfactor from joined")
risk_factor_spark.registerTempTable("risk_factor_spark")
risk_factor_spark.collect.foreach(println)
hiveContext.sql("create table finalresults( driverid String, occurance bigint,totmiles bigint,riskfactor double) stored as orc").toDF()
\\ write to ORC format
risk_factor_spark.write.orc("risk_factor_spark")
hiveContext.sql("load data inpath 'risk_factor_spark' into table finalresults")
hiveContext.sql("select * from finalresults")
Run Spark commands in shell (load Scala API) : $ spark-shell
- PySpark
- PySpark API Docs
-
Spark Progamming Guide
- SparkConf: for configuring Spark
- SparkFiles: access files shipped with jobs
- SparkContext: main entry point for Spark functionality
- RDD: basic abstraction in Spark
- Broadcast: a broadcast variable that gets reused across tasks
- Accumulator: an “add-only” shared variable that task can only add values to
- StorageLevel: finer-grained cache persistence levels
# Word Count example
from pyspark import SparkConf, SparkContext
conf = SparkConf().setMaster("local").setAppName("WordCount")
sc = SparkContext(conf = conf)
input = sc.textFile("file:///sparkcourse/book.txt")
words = input.flatMap(lambda x: x.split())
wordCounts = words.countByValue()
for word, count in wordCounts.items():
cleanWord = word.encode('ascii', 'ignore')
if (cleanWord):
print cleanWord, count
Reference
08 Apr 2016
Notes for Data Wrangling with MongoDB from Udacity
We need to assess our data to:
- Test assumptions about: values, data types, and shape
- Identity errors or outliers
- Find missing values
CSV is lightweight:
- Each line of text is a single row
- Fileds are seperated by a delimeter
- Just the data itself
- Don’t need special software
- All spreadsheet apps read/write CSV
Data Modeling in JSON
- Items may have different fields
- May have nested objects
- May have nested arrays
XML desgin goals
- Data transfer
- Easy to write code to read/write
- Document valiation
- Human readable
- Supports a wide variety applications
Measures of data quality
- Validity: conforms to a schema
- Accuracy: conforms to gold standard
- Completeness: all records
- Consistency: matches other data
- Uniformity: same units
Blueprint for cleaning data
- Audit your data
- Create a data cleaning plan
- Execute the plan
- Manually correct
Inequality operators for MongoDB: $gt, $lt, $gte, $lte, $ne.
# Find cities with population > 2500, but <= 50000.
# Ineuqality operators also work for strings and dates.
query = {"population": {"$gt": 2500, "$lte", 50000}}
cities = db.cities.find(query)
# Update all documents in database
city = db.cities.update({"name": "Munchen", "country": "Germany"},
{"$set": {"isoCountryCode": "DEU"}},
multi=True)
Other MongoDB operators:
- $in: if in certain sets
- $exists: if certain value exists or not
- $all: must contain all the values
- $and: two conditions must all satisfy
In MongoDB shell:
# First part is query condition, second part is projection for output format.
db.tweets.find({"entities.hashtags": {"$ne": []}}, {"entities.hashtags.text": 1, "_id": 0})
# remove all cities that don't have names
db.cities.remove({"name": {"$exists": 0}})
Aggregation framework in MongoDB
Example: who tweeted most?
- Group Tweents by user
- Count each users tweets
- Sort into descending order
- Select user at top
# realize the above process through pipeline.
result = db.tweets.aggregate([
{"$group": {"_id": "$user.screen_name", "count": {"$sum": 1}}},
{"$sort": {"count": -1}}])
Use $project to:
- Include fields from the original document
- Insert computed fields
- Rename fields
- Craete fields that hold subdocuments
# Question: who has the highest followers_to_friends ratio?
# Match operator
result = db.tweets.aggregate([
{"$match": {"user.friends_count": {"$gt": 0},
"user.followers_count": {"$gt": 0}}},
{"$project": {"ratio": {"$divide": ["$user.followers_count",
"$user.friends_count"]},
"screen_name": "$user.screen_name"}},
{"$sort": {"ratio": -1}},
{"$limit": 1}])
Use $unwind :
result = db.tweets.aggregate([
{"$unwind": "$entities.user_mentions"},
{"$group": {"_id": "$user.screen_name",
"count": {"$sum": 1}}},
{"$sort": {"count": -1}},
{"$limit": 1}])
$group operators: $sum, $first, $last, $max, $min, $avg.
result = db.tweets.aggregate([
{"$unwind": "$entities.hashtags"},
{"$group": {"_id": "$entities.hastags.text",
"retweet_avg": {"$avg": "$retwet_count"}}},
{"$sort": {"retweet_avg": -1}},
{"$limit": 1}])
Array operators: $push, $addToSet
result = db.tweets.aggregate([
{"$unwind": "$entities.hashtags"},
{"$group": {"_id": "$user.screen_name",
"unique_hashtags": {"$addToSet": "$entities.hashtags.text"}}},
{"$sort": {"_id": -1}},
More aggregation operators can be found here.
07 Apr 2016
1. Machine Learning to Deep Learning
Logistic classifier: $wx + b = y$, w is weight, x is input, b is bias.
Softmax: $S(y_i) = \frac{e^{y_i}}{\sum_j e^{y_j}}$ turn scores into probabilities.
- If multiply the scores by 10, the probabilities get close to either 0 or 1.
- If divided by 10, the probabilities get close to uniform.
Cross-entropy: $D(S,L) = -\sum_i L_i log(S_i)$, S is socre, L is lable.
Multinomial logistic classification:linear model $wx+b$ -> logit score -> softmax S(y) -> Cross-entropy D(S,L) -> 1-hot labels.
Loss = average cross-entropy: $\frac{1}{N} \sum_i D(S(wx_i +b), L_i)$.
Minimize traning loss using gradient descent method.
Input is typically normalized, weights are typically initilized with random values from Gaussian distribution.
Training, validation, test datasets.
Rule of thumb for validation set size: A change that affects 30 examples in your validation set, one way or another, is usually statistically significant and typically can be trusted.
Use stochastic gradient descent to make the optimization process faster, which is the core of deep learning.
Two methods to help SGD faster:
- Momentum: for SGD, each step we take a very small step in a random direction, but on aggregate, those steps take us toward the minimum of the loss. We can take advantage of the knowledge that we’ve accumulated from previous steps about where we should be headed. A cheap way to do that is to keep a running average of the gradients, and to use that running average instead of the direction of the current batch of the data. M <- 0.9M + $\Delta \alpha$.
- Learning rate decay: when replacing gradient descent with SGD, we are going to take smaller, noiser steps towards our objective. It is hard to decide how smaller that step should be. However, it is beneficial to make that step smaller and smaller as you train.
Learning rate tuning: plot the loss and step figures. Never trust how quickly you learn, it has often little to do with how well you train.
SGD hyper-parameters: initial learning rate, learning rate decay, momentum, batch size, weight initilization.
When things don’t work, always try to lower the learning rate first.
AdaGrad is a modification of SGD which implicitly does momentum and learning rate decay for you. Using AdaGrad often makes learning less sensitive to hyper-parameters. But it often turns to be a litte worse than precisely tuned SDG with momentum.
2. Deep Neural Networks
Backward propagation - use chain rule.
You can typically get much more performance with fewer parameters by going deeper rather than wider. A lot of natural phenomena tend to have a hierarchical structure which deep models naturally capture.
Prevent overfitting:
- Early termination: look at the performance under validation set, and stop training as soon as no further improvement.
- Regularization: apply artifical constraints that implicitly reduce the number of free parameters while not making it more difficult to optimize, such as L2 regulization.
- Dropout: Imagine that you have one layer that connects to another layer. The values that go from one layer to the next are often called activiations. Take those activations and randomly for every example you train your network on, set half of them to zero. Basically, you randomly take half of your data through your network and just destroy it, and then randomly again. Learn from reduntant representations. More robust, and prevent overfitting.
3. Convolutional Neural Networks
Translation invariance: different places, but same objective.
Weight sharing: when you know that two inputs can contain the same kind of information, then you share the weights and train the weights jointly for those inputs.
CNN is network that share parameters across space.
Patches are sometimes called kernels. Each pancake in stack is called a feature map. Stride is the number of pixels that you shift each time you move the filter.
- Valid padding: do not go past the edge.
- Same padding: go off the edge and pad with zeros.
Pooling: Until now, we’ve used striding to shift the filters by a few pixel each time and reduce the future map size. This is a very aggresive way to downsample an image. It removes a lot of information. What if instead of skipping one in every two convolutions, we still ran with a very small stride, but then took all the convolutions in a neighborhood and combined them somehow. This is called pooling. The most common one is max pooling. At every point in the future map,look at a small neighborhood around that point and compute the maximum of all the responses around it. Max pooling doesn’t add number of parameters, and doesn’t risk an increasing overfitting. It simply often yields more accurate models. However, since the convolutions that run below run at a lower stride, the model becomes a lot more expensive to compute, and there are some paramters to set, such as pooling size and stride. Another notable form of pooling is average pooling. Instead of taking the max, just take an average over the window of pixels around a specific location.
1x1 convolutions: The classic convolution setting is basically a small classifier for a patch of the image, and it’s only a linear classifier. But if you add a 1x1 convolution in the middle, then you have a mini neural network running over the patch instead of a linear classifier. This is a very inexpensive way to make your models deeper and have more parameters without completely changing their structure. Actually, they are just matrix multiplies which have relative few parameters and computationaly cheap.
Inception module: Instead of having a single convolution, we put the pooling and 1x1 convolution or nxn convolution together. We can choose parameters in such a way that the total number of parameters in model in very small. Yet the model performs better.
4. Deep Models for Text and Sequences
Embeddings: put similar words into a smaller set.
t-SNE: a way of projections that preserves the neighborhood structure of data.
Distance: because of the way embeddings are trained, it’s offten better to measure the closeness using a cosine distance instead of L2 and normalized.
Sampled softmax: Instead of treating the softmax as if the label had probability of 1, and every other word has probability of 0, we can sample the words that are not the targets, pick only a handful of them and act as if the other words were not there. It makes things faster at no cost in performance.
Semantic analogy can make word vectors do the math.
Simiar as Covolutional Neural Network (CNN) uses shared parameters across space to extract patterns over an image, Recurrent Neural Network (RNN) (handle word sequence) does the same thing but over time instead of space.
Imagine that you have a sequence of events, at each point in time you want to make a decision about what’s happened so far in the sequence. If your sequence is reasonably stationary, you can use the same classifier
at each point in time. That simplifies things a lot already. But since this is a sequence, you also want to take into account the past. One natural thing to do here is to use the state of the previous classifier as a summary of what happened before, recursively.
Backpropagation for RNN will apply all updates to the same parameters (correlated updates), which is very unstable and bad for SGD. The gradients either go exponentially to infinity or zeros very quickly, which is called exploding and vanishing gradient problem, respectively.
Exploding gradients: use gradient clipping (shrink step when gradient norm goes too big) to handle the gradient bounding problem. $\Delta w = \Delta w \frac{\Delta_{max}}{max(\vert \Delta w \vert, \Delta_{max})}$
Vanishing gradients makes model only remeber recent events, which is “memory-loss”. This is where Long Short Term Memeory (LSTM) comes to help.


LSTM regulization: L2 and Dropout
RNN can be used to generate sequences.
Imagine that you have a model that predicts the next step of your sequence. You can use that to generate sequences. You sample from the predicted distribution and then pick one element based on its probability, and then feed to the next step and go on. Do this repeatedly, you can generate a pretty good sequence. A more sophisticated way is instead of sampling once at each step, sample multiple times. Choose the best sequence out of those by computing the total probability of all the characters that you generated so far. This can prevent the sampling from accidentally making one by choice, and being stuck with the one bad decision forever. A smarter way to do this is called Beam Search, which only keep the mostly likely few candidate sequences at every time step, and simply prune the rest. This works very well in practice.
06 Apr 2016
1. Introduction
- Belief = probability
- Sense = product followed by normalization
- Move = convolution (addition)
localization: sense-move cycle.
Entropy = $-\sum_i p(x_i) log(p(x_i))$
Total probability: $P(A) = \sum_iP(A\vert B_i) P(B_i)$, which is also called convolution.
Bayes Rule: $P(A\vert B) = \frac{P(B\vert A) P(A)}{P(B)}$
2. Kalman Filters
- Kalman filter: continous, uni-modal
- Monte Carlo localization: discrete, multi-modal
- Partical filter: continous, multi-modal
1-D Gaussian: $f(x) = \frac{1}{\sqrt{2\pi{\sigma}^2}}e^{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}}$
In Kalman Filter:
- Measurment update: product, Bayes rule
- Motion update (Prediction): convolution (addition), Total Probability
- Gaussian is used to combine them together
Mutiply two Gaussians with $\mu_1, \sigma_1^2$ and $\mu_2, \sigma_2^2$, we have the new Guassian with
- $\mu = \frac{\sigma_2^2 \mu_1 + \sigma_1^2 \mu_2}{\sigma_2^2+\sigma_1^2}$
- $\sigma^2 = \frac{1}{\frac{1}{\sigma_2^2}+\frac{1}{\sigma_1^2}}$
- This is the measurement update.
Motion update: $\mu_{new}$ <- $\mu + \nu$; $\sigma_{new}^2$ <- $\sigma^2+ \gamma^2$.
Kalman Filter can map states from “Observable” to “Hidden”.
Suppose x is estimate, P is uncertainty covariance, F is state transition matrix, u is motion vector, Z is measurement, H is measurement function, R is measurement noise, I is identity matrix, then we have
- prediction: $x’ = Fx+u$; $P’=FPF^T$
- measuremnt update: $y=Z-Hx$; $S=HPH^T+R$; $K=PH^TS^{-1}$; $x=x+KY$; $P’ =(I-KH)P$.
3. Particle Filters
| |
state space |
belief |
efficiency |
in robotics |
| Histogram Filter |
discrete |
multimodal |
exponential |
approximate |
| Kalman Filter |
continous |
unimodal |
quadratic |
approximate |
| Particle Filter |
continuous |
multimodal |
? |
approximate |
Key advantageof Particle Filter is easy to program.
Resampling: Resample the particles with replacement and probability proportional to the importance weights.
- Measurement updates: $P(x\vert z) \propto P(z\vert x) P(x)$
- Motion updates: $P(x’) = \sum P(x\vert x) P(x)$
- $P(x)$ is particles; $P(z\vert x)$ is importance weights; $P(x’\vert x)$ is sample
4. Search
Planning problem: Given map, starting location, goal location, and cost, find minimum cost path.
A-search: heuristic function is the optiaml guess of how far from the goal (withou obsticles)
Dynamical Progamming
5. PID Control
Smoothing algorithms: minimize $(x_i - y_i)^2 + \alpha (y_i - y_{i+1})^2$ using gradient descent.
- P controller: steering = $-\tau_P * CTE$, CTE means cross track error.
- PD controller: steering = $-\tau_P * CTE - \tau_D * \frac{dCTE}{dt}$
- PID controller: steering = $-\tau_P * CTE - \tau_D * \frac{dCTE}{dt} - \tau_I * \sum CTE$
- P is proportional, to minimize error; I is integral, to compliment drift; D is differential, to avoid overshoot.
Twiddle (coordiane descent): run() -> goodness
# twiddle algorithm
def twiddle(tol = 0.2):
#Make this tolerance bigger if you are timing out!
############## ADD CODE BELOW ####################
n_params = 3
dparams = [1.0 for row in range(n_params)]
params = [0.0 for row in range(n_params)]
best_error = run(params)
n = 0
while sum(dparams) > tol:
for i in range(len(params)):
params[i] += dparams[i]
err = run(params)
if err < best_error:
best_error = err
dparams[i] *= 1.1
else:
params[i] -= 2.0 * dparams[i]
err = run(params)
if err < best_error:
best_error = err
dparams[i] *= 1.1
else:
params[i] += dparams[i]
dparams[i] *= 0.9
n += 1
print 'Twiddle #', n, params, '->', best_error
print ' '
return run(params)
6. SLAM
Simultaneous localizations and mapping (SLAM)
03 Apr 2016
1. Decision Trees
Supervised Learning:
- Classification: output discrete
- Regression: output continuous
Classification learning:
- Instances (Input)
- Concepts (Functions)
- Targets
- Hypothesis
- Sample (training set)
- Candidate
- Testing set
Decision Trees Learning:
- Pick best attribute
- Ask questions
- Follow the answer path
- Repeat the process unitl get the answer
ID3: find for each node the categorical feature that will yield the largest information gain for categorical targets.
ID3 algorithm:
- A <- best attribute
- Assign A as decision attribute for node
- Fore each value of A, create a descendant of node
- Sort training examples to leaves
- If example perfectly classified, STOP; else iterate over leaves.
- Loop the whole process until STOP.
- Prone if overfitting
Gain(S, A) = Entropy(S) - $\sum_r \frac{\vert S_r \vert}{\vert S\vert}Entropy(S_r)$
Entropy = $-\sum_rP(r)log(P(r))$
ID3 Bias: restrictive bias (hypothesis), preference bias(inductive bias).
2. Regression
3. Neural Network
Given example, find weights that map inputs to outputs
- perception rule (threshold)
- gradient decent rule (unthresholded)
Perception rule (single unit):
$ w_i = w_i +\Delta w_i$
$ \Delta w_i = \eta (y-\hat{y}) x_i $
$ \hat{y} = (\sum w_i x_i \le 0) $
$y$ is target; x is input; $\hat{y}$ is output $\eta$ is learning rate.
Gradient descent:
$ \hat{y} = a = \sum x_i w_i $
$ E(w) = \frac{1}{2} \sum (y-a)^2$
$ \frac{\partial E}{\partial w_i} = \sum(y-a)(-x_i) $
Comparison of learning rules:
- perception: guarantee finite convergences linear seperatability
- gradient descent: calculus robust, converge local optimal
Sigmoid function $ \sigma(a) = \frac{1}{1+e^{-a}}$, is the differentiable threshold.
So the whole structure of neural networks is differentiable.
Backpropogation:
- Computationally beneficial organizaiton of the chain rule
- Many local optimal
Optimizing weights:
- gradient descent
- momentum method
- higher order derivatives
- random optimization
- penalty for “complexity”
Restriction bias:
- representation power
- set of hypothesis we will consider
- perception: half spaces
- sigmoid: much more complex, not much restriction
Neual networks can represent:
- boolean functions: network of threshold-like units
- continous functions: “connected” no jumps - 1 hidden layer
- artibitrary functions: stitch together - two hidden layers
We need to use methods like cross-validation to avoid overfitting.
Preference bias: algorithms selection of one representation over another
Initiall weights: small random values, small means low complexity, random may avoid local minimums.
DO NOT make more complex network unless you can get smaller error.
4. Instance based learning
Put all data into a database, do a look up.
- remember extactly
- fast and simple
- no generalizations
K-NN(K nearest neighor):
Given: training data D = {$x_i, y_i$}; distance metric d(q, x), number of neighbors k, query point q.
NN = {i: d(q, $x_i$) k smallest}
Return:
- classification: weighted vote of the $y_i \in$ NN
- regression: weighted mean of the $y_i \in$ NN
K-NN bias:
- perference bias: our belief about what makes a good hypothesis
- locality: near points that are similar
- smoothness: averaging
- all featrues matter equally
Curse of dimensionality:
As the number of features or dimensions grow, the amount of data we need to generalize accurately grows exponentially!
For machine learning, that means more data and less features.
5. Ensemble learning: boosting
- Learn over a subset of data -> get rules
- Combine them together to get the generalized rule
Ensemble methods:
- Bootstrap:
- Given a dataset of size N;
- Draw N samples with replacement to create a new dataset;
- Repeat ~1000 times and get ~1000 sample datasets;
- Compute ~1000 sample statistics.
- Bagging:
- Draw N bootstrap samples;
- Retrain the model on each sample;
- Average the results (for regression, do averaging; for classification, do majority vote);
- Works great for overfit models (decrease variance without changing bias; doesn’t help much with underfit/high bias model)
- Boosting:
- Instead of selecting data randomly with the bootstrap, favor the misclassified points
- Initialize the weights
- Repeat: resample with respect to weights; retrain the model; recompute weights
Ensemble method combines simple models with bad resutls together to get better results. To me, it’s like the diverse investiment theory in finance. By diversifying your investiment, you can get lower risk.
Boosting error estimate: instead of using number of mismatches, the probability of each mismatche $P[h(x) \ne c(x)]$ will be considered.
“Weak” learner: does better than change always. For all data distribution, error rate is less than half.
Boosting for binary classificatin (AdaBoost):
- Given traning examples $(x_i, y_i)$, $y_i$ in {-1, 1}
- Initialize $D_1(i) = 1/m$.
- For t = 1 to T
- Train weaker learner using distribution $D_t$
- Get weak classifier $h_t$
- Choose $\alpha_t$
- Update $D_{t+1}(i) = \frac{D_t(i) exp{-\alpha_t y_i h_t(x_i)}}{Z_t}$, where $\alpha_t = \frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t})$, $Z_t$ is normalization factor $Z_t = \sum_i D_t(i) exp(-\alpha_t y_i h_t(x_i))$.
- Output final classifier: $H(x) = sign(\sum_{t=1}{T} \alpha_t h_t(x))$.
The weak learner’s job is to find a weak classifier $h_t$ for the distribution $D_t$. In the binary case, it is to minimize the error $\epsilon_t = P[h_t(x_i) \ne y_i]$.
For boosting, it’s much harder to get overfitting.
A nice overview of boosting method: The Boosting Approach to Machine Learning An Overview.
Here are some notes from that paper.
Boosting is based on the observation that finding many rough rules of thumb can be a lot of easier than finding a single, highly accurate prediction rule. To apply the boosting approach, we start with a method for finding the rough rules of thumb, which is called “weak” or “base” learner, repeatedly. Each time we feed it a different subset of the training exammples with different distribution or weighting. The “weak” learner generates a new weak prediction rule. After many rounds, the boosting mehtod must combine these weak rules into a single prediction rule that will be much more accurate than any one of the weak rules.
Like I mentioned before, the principle is similar as the diversifying investiment strategy, by doing that you can get lower risk than each strategy does.
To make the boosting approache work, two questions must be answered:
- how should each distribution be chosen on each round?
- how should the weak rules be combined into a single rule?
Regarding the choice of distribution, the method is to place most weight on the examples most offten misclassified by the preceding weak rules, which forces the weak learner to focus on the “hardest” examples. For combing weak rules, a natural and effective way is taking a (weighted) majority vote for their prediction.
Boosting method may avoid overfitting, because it’s like the SVMs by increasing the margins. It tends to overifft if weak learner uses ANN with many layers and nodes.
- Pink noise: uniform noise
- White noise: Guassian noise
6. Kernel methods and Support Vector Machines
$y = w^T x + b$ , y is classification label, w and brepresenet parameters of the plane.
$ w^T x+ b = 0$ is the decision boundary.
$ w^T x + b = \pm 1$ are the margin.
$ \frac{w^T}{|w|}(x_1 - x_2 = \frac{2}{|w|})$, the l.h.s is the margin we need to maximize while classifying everything correctly $y_i (w^T + b) \ge 1, \forall i$.
That is equal to minimize $1/2 |w|^2$, which makes optimization problem easier.
It turns out it also equals to maximize $W(\alpha) = \sum_i \alpha_i - 1/2 \sum_{i.j} \alpha_i \alpha_j y_i x_i^T x_j, s.t., \alpha_i \ge 0, \sum_i \alpha_i y_i = 0$. So we can get $w = \sum \alpha_i y_i x_i$ and b. It turns out that $\alpha_i$ mostly are zeros. That means only a few points matter.
We can use kernel functions to represent the similarity, and solve the problem in a different dimension.
7. Computational learning theory
Computatioanl learning theory:
- define learning problems
- show specific algorithms work
- show thesse problems are fundamentally hard
Theory of computing analyzes how algorithms use resourse: time, space et .
Defining inductive learning - learning from examples:
- probability of successful training
- number of examples to train on
- complexity of hypothesis class
- accuracy to which target concept is appropriate
- manner in whihch training examples presented (batch, online)
- manner in which training examples selected
Select training examples:
- Learner asks questions of teacher
- Teacher gives examples to help learner
- Fixed distribution
Teacher with constrained queries:
- X: x1, x2, …, xk; k-bit input
- H: conjunctions of literals or negation
Computationl complexity: how much computational effort is needed for a learner to change?
Sample comoplexity - batch: how many training examples are needed for a learner to create successful hypothesis?
Mistake bounds - online: how many misclassifications can a learner make over an infinite run?
PAC learning - error of hypothesis:
- Training error: fraction of training examples misclassified by h
- True error: fraction of examples that would be misclassified on sample draw from D
$error_D(h) = P_{x~D}[c(x) \ne h(x)]$
Notations:
- C: concept class
- L: learner
- H: hypothesis space
- n: size of hypothesis space
- D: distribution over inputs
- $0\le \epsilon \le 1/2 $: error goal
- $0 \le \sigma \le 1/2 $: certainty goal ($1-\sigma$)
C is PAC-learnable by L using H if learner L will, with probability $1-\epsilon$, output a hypothesis $h \in H$ s.t. $error_D(h) \le \epsilon$ in time and spae and samples polynomial in $1/\epsilon, 1/\sigma$ and n.
VS(s) is the set of trainning hypotheses in H that perfectly fit the training data.
VS(s) is $\epsilon$-exhuasted iff $\forall h \in$ VS(s), $error_D(h) \le \epsilon$.
Haussler Theorem - Bound True Error: Let $error_D(h_1,…, h_k \in H) > \epsilon$ be the high true error, how much data do we need to “knock off” these hypothesis?
$ P(h_i(x) = c(x)) \le 1-\epsilon$, if everything is independent, we have P($h_i$ consistent with c on m exmaples) $\le (1-\epsilon)^m$. P(at least one of $h_i$ consistent with c on m exmaples) $\le k(1-\epsilon)^m \le \vert H\vert (1-\epsilon)^m \le \vert H\vert e^{-\epsilon m} \le \delta$. This is the upper bound that version space is not $\epsilon$-exhusted after m samples. That is, $m \le \frac{1}{\epsilon} (ln(\vert H\vert) + ln \frac{1}{\delta})$.
Because $-\epsilon \ge ln(1-\epsilon)$, $(1-\epsilon)^m \le e^{-\epsilon m}$.
If H is finite, and m is a sequence of independent randomly drawn training points, then for any $0 \le \epsilon \le 1$, the probability that the version space is not $\epsilon$-exhausted is bounded above by $\vert H\vert e^{-\epsilon m}$.
8. VC dimensions
Infinite hypothesis spaces: linear separators, ANN, continuous decision trees.
VC dimension: the size of the largest subset of input that the hypothesis class can shatter, it can be considered a measure of complexity of a hypothesis space.
For d-dimensional hyperplane, the VC dimensionis d+1.
Sample complexity and VC dimension: $m \ge \frac{1}{\epsilon} (8 VC(H) log_2 \frac{13}{\epsilon}+4log_2^{\frac{2}{8}})$ for infinite case, $m \ge (ln(\vert H\vert) + ln(\frac{1}{8}))$ for finite case.
For finite case, $d \le log_2(\vert H\vert)$.
H is PAC-learnable if and only if VC dimension is finite.
9. Bayesian learning
Bayesian learning: learn the most probable hypothesis given data and domain knowledge.
$P(h\vert D) = \frac{P(D\vert h)P(h)}{P(D)}$
$P(a,b) = P(a\vert b) P(b) = P(b\vert a) P(a)$
P(D\vert h) is data given the hypothesis, P(h) is the prior on data, P(D) is prior on data.
For each $h \in H$, calculate $P(h\vert D) = P(D \vert h) P(h) / P(D)$.
Output (suppose P(h) is uniform):
- map -> maximum posterior: $h_m = argmax P(h\vert D)$
- machine learning -> maximum likelihood: $h_{ML} = argmax P(D\vert h)$.
10. Bayesian inference
- Representing and resasoning with probabilities
- Bayesian Networks
X is conditionally independent of Y given Z if the probability distribution governing X is independent of the value of Y given the value of Z; that is $P(X\vert Y,Z) = P(X\vert Z)$.
Belief Networks aka Bayesian Networks aka Graphical Models
Why sampling?
- get probability of values, and generate values for certain distribution
- simulation of a complex process
- approximate inference
- visualization
Inferencing rules:
- Marginalization: $P(x) = \sum_y P(x, y)$
- Chain rule: P(x, y) = $P(x)P(y\vert x)$
- Bayes rule: $P(y\vert x) = P(x\vert y)P(y)/P(x)$
11. Randomized optimization
Optimization:
Input space X, objective function f(x), goal is to find $\hat{x} \in X$ s.t. $f(\hat{x})=max f(x)$.
Optimization approaches:
- Newton methods: single optimum problem wit derivatives
- Randomized optimization: big input space, complex function, no derivative or hard to find.
Hill climbing:
- Guess $x \in X$
- Repeat:
- let $x^* = argmax f(x)$ for $x \in N(x)$, N means neighborhood
- if $f(x^*) > f(x)$: x = n
- else: stop
Randomized hill climping: once local optimum is reached, try gain starting from a randomly chosen x.
Advantages: multiple tries to find a good starting place, not much more expensive (constant factor).
Simulated Annealing: don’t always improve, sometimes you need to search (explore).
For a finite set of iterations:
- Sample new point $x_+$ in N(x)
- Jump to new sample with probability given by an acceptance probability function $P(x, x_+, T)$
- Decrease temperate T
$P(x, x_+, T) = 1$, if $f(x_+) \ge f(x)$
$P(x, x_+, T) = e^{\frac{f(x_+)-f(x)}{T}}$, otherwise.
Properties of Simulated Annealing:
- T -> $\infty$ means likely to move freely (random wal), T -> 0 means go uphill.
- P(ending at x) = $\frac{e^{f(x)/T}}{Z_T}$ Boltzman distribution
Genetic Algorithms (GA):
mutation - local search; cross over - population holds information; generations - iterationos of improvement.
# GA skeleton
P0 = initial population of size K
repeat until converged
compute fitness of all x
select "most fit" individuals (top half, weighted probability)
pair up individuals, replacing "least fit" individuals via crossover/mutation
The above methods:
- only points, no structure
- unclear probability distribution
MIMIC method: convey structure, direct model distribution.
$P^{\theta}(x) = \frac{1}{z_{\theta}}$, if $f(x) \ge \theta$
$P^{\theta}(x) = 0 $, otherwise
$P^{\theta_{min}}(x) = uniform$; $P^{\theta_{max}}(x) = optima$
MIMIC pseudo code:
Generate samples from $P^{\theta}(x)$;
Set $\theta_{t+1}$ to nth percentice;
Retain only those samples s.t. $f(x) \gt \theta_{t+1}$;
Estimate $P^{\theta_{t+1}}(x)$;
Repeat.
12. Clustering
Basic clustering problem:
- Given set of object x, inter-object distance D(x,y) = D(y,x)
- Output: partition $P_D(x) = P_D(y)$ if x and y in same cluster
Single linkage clustering (SLC):
- consider each object a cluster (n object)
- define intercluster distance as the distance between the closest two points in the two clusters
- merge two closet clusters
- repeat n-k times to make n cluster
Runing time of SLC with n points and k clusters is $O(n^3)$.
K-means clustering:
- pick k centers at random
- each center claims its closest points
- recompute the centers by averaging the clustered points
- repeat until convergence
Properties of K-means clustering:
- each iteration polynomial O(kn)
- finite (exponential) iterations $O(k^n)$
- error decreases if ties broken consistently
- can get stuck (local optima)
Soft clustering:
- Assume the data was generated by
- select one of k Gaussians uniformly
- sampel $x_i$ from that Gaussian
- repeat n times
- Task: find a hypothesis that maximizes the probability of the data
The machine learning mean of the Gaussian mean is the mean of the data.
Expectation maximization:
Properties of EM:
- monotonically non-decreasing likelihood
- does not have to converge (practically does)
- will not diverge
- can get stuck
- works with any distribution (if EM solvable)
Clustering properties:
- Richness: for any assignment of objects to clusters, there is some distance matrix D s.t. $P_D$ returns that clustering $\forall c \in D$, $P_D=c$.
- Scale-invariance: scaling distance by a positive value doesn’t change the clustering.
- Consistency: shrinking intracluster distances and expanding intercluster distance does not change the clustering.
Impossibility theorem: no clustering scheme can achieve all three of richness, scal invariance, and consistency.
13. Feature selection
- Knowledge discovery
- Curse of dimensionality
Two methods:
- filtering: faster, isolated featrues, ignores the learning problem
- information gain, variance, entropy
- wrapping: takes into account model bias, slow
- hill climping, randomized optimization, forward, backward
Relevance
- $x_i$ is strongly relevant if removing it degrades Bayes Optimal Classifier(BOC)
- $x_i$ is weakly relevant if
- not strongly relevant
- there’s a subset of features s.t. adding $x_i$ to this subset improves BOC
- otherwise, $x_i$ is irrelevant
The problem of pre-processing a set of features to create a new feature set, while retaining as much information as possible.
- PCA: correlation, maximize variance
- ICA: independence of new feature
- RCA: generate random directions
- LDA: linear discriminant analysis, find a projection that descriminates based on the label
- Mutual information: are the input vectors similar?
- Entropy: does each feature have any information?
Entropy: $H(x) = -\sum P(x) logP(x)$
Joint Entropy: $H(x,y) = -\sum P(x, y) logP(x,y)$
Conditional Entropy: $H(y \vert x) = -\sum P(x, y) logP(y \vert x)$
Mutual Information: $I(x,y) = H(y) - H(x \vert y)$
KL divergence: measure distance between two distributions $D(p \vert q) = \int p(x) log(\frac{p(x)}{q(x)})$
16. Markov decision process
- State: s
- Model: $T(s,a,s’) ~ P(s’ \vert s, a)$
- Actions: A(s), A
- Reward: R(s), R(s,a), $R(s,a,s’)$
- Policy: $\Pi(s)$ -> a, $\Pi^*$ is the optimal policy.
Sequence of rewards
- infinite horizons -> stationary
-
Utility of sequeneces -> stationary preference, if $U(s_0, s_1, \ldots) > U(s_0, s_1^{'}, \ldots)$, then $U(s_1, \ldots) > U(s_1^{'}, \ldots)$.
- $U(s_0, s_1, s_2, \ldots) = \sum_{t=0}^{\inf} R(s_t)$. This cannot tell the difference between two sequences if they all go to infinity
- $U(s_0, s_1, s_2, \ldots) = \sum_{t=0}^{\infty} \gamma^t R(s_t) \le \sum_{t=0}^{\infty} \gamma^t R_{max} = \frac{R_{max}}{1-\gamma}$, $0 \le \gamma <1$. This is similar as the utility definition in economics.
Polices - Bellman Euqation:
-
$\Pi^* = argmax_{\Pi} E[\sum_{t=0}^{\infty} \gamma^t R(s_t) \vert \Pi]$
-
$ P^{\pi}(s) = E[\sum_{t=0}^{\infty} \gamma^t R(s_t) \vert \Pi, s_0 = s]$
-
$\Pi^* = argmax_{a} \sum_{s’} T(s,a,s’) U(s’)$
-
$U(s) = R(s) + \gamma \max_a \sum_{s’} T(s, a, s’) U(s’)$
Reward is immediate, and utility is long-term reward.
Value iteration:
- start with arbitrary utility
- update utility based on neigbors
- repeat until converge
Policy iteration:
- start with $\pi_0$ by guessing
- evaluate: given $\Pi_t$ calculate $u_t^{\Pi}$
- improve $\Pi_{t+1}=argmax_a \sum T(s,a,s’) U_t(s’)$
- $ U_t(s) = R(s) + \gamma \sum_{s’} T(s, \Pi_t(s), s’) U_t(s’)$
The Bellman Equation:
- $V(s) = \max_a(R(s,a) + \gamma \sum_{s’}T(s,a,s’)V(s’))$, V here is the value function.
- $Q(s,a) = R(s,a) +\gamma \sum_{s’}T(s,a,s’) \max_{a’} Q(s’,a’)$, Q is quanlity
-
$C(s) = \gamma \sum_{s’} T(s,a,s’) \max_{a’}(R(s’,a’)+C(s’,a’))$, C is the continuation.
- $V(s) = \max_aQ(s,a)$
- $V(s) = \max_a(R(s,a) + C(s,a))$
- $Q(s,a) = R(s,a) + \gamma\sum_{s’}T(s,a,s’) V(s’)$
- $Q(s,a) = R(s,a) +C(s,a)$
- $C(s,a) = \gamma \sum_{s’}T(s,a,s’)V(s’)$
- $C(s,a) = \gamma \sum_{s’}T(s,a,s’)\max_{a’}Q(s’,a’)$
17. Reinforcement learning
Three approaches to RL:
- Policy search: direct use indirect learning s->$\Pi$->a
- Value-function based: s->U->v
- Model-based: direct learning indirec use <s,a> -> <T, R> -> <s’, r>
A new kind of value function:
- $ U(s) = R(s) + \gamma \max_q \sum_{s’} T(s, a, s’) U(s’)$
- $ \Pi(s) = argmax_a \sum_{s’} T(s, a, s’) U(s’)$
Q-learning:
- $ Q(s, a) = R(s) + \gamma \sum_{s’} T(s, a, s’) \max_{a’}Q(s’,a’)$, value for arrving in s, leaving via a, proceeding optimaally thereafter.
- $ U(s) = \max_a Q(s,a) $
- $ \Pi(s) = argmax_a Q(s,a) $
$\hat{Q}(s,a) = (1-\alpha_t) (R(s)+ \gamma \max_{a’}\hat{Q}(s’,q’))+\alpha_t (R(s)+ \gamma \max_{a’}\hat{Q}(s’,q’))$
Q-learning is a family of algorithms:
- how initialize $\hat{Q}$?
- how decay $\alpha_t$?
- how choose actions?
$\epsilon$-Greedy exploration: “greedy limit + infinite exploration”, exploration-exploiation dilemma.
Temporal Difference Learning: learn to predict over time
Properties of learning rates: $V_T(s) = V_{T-1}(s) + \alpha_T(R_T(s)-V_{T-1}(s))$; $ \displaystyle \lim_{T \to \infty}V_T(s) = V(s)$; $\sum_T \alpha_T=\infty, \sum_T\alpha_T^2 <\infty$.
TD(1) Rule:
-
Episode T
-
For all s, e(s) = 0 at start of episode, $V_T(s) = V_{T-1}(s)$
-
After $s_{T-1}$->$s_T$ with reward $r_t$: $e(s_{T-1})=e(s_{T-1})+1$
-
For all s,
- $V_T(s) = V_T(s) + \alpha_T (r_t + \gamma V_{T-1}(s_t)-V_{T-1}(s_{T-1}))e(s)$; $e(s) = \gamma e(s)$
$TD(\lambda)$ Rule:
- Episode T
- For all s, e(s) = 0 at start of episode, $V_T(s) = V_{T-1}(s)$
- After $s_{T-1}$->$s_T$ with reward $r_t$: $e(s_{T-1})=e(s_{T-1})+1$
- For all s,
- $V_T(s) = V_T(s) + \alpha_T (r_t + \gamma V_{T-1}(s_t)-V_{T-1}(s_{T-1}))e(s)$; $e(s) = \lambda \gamma e(s)$
Bellman operator: let B be an operator, or mapping from value functions to value functions $BQ(s,a)=R(s,a) +\gamma \sum_{s’}T(s,a,s’) \max_{a’}Q(s’,a’)$; $Q^{*}=BQ^{*}$ is Bellman Equation; $Q_T=BQ_{T-1}$ is Value Iteration.
Contraction Mappings: B is an operator, if for all F, G and some $0 \le r <1$, $\vert BF-BG\vert _{\infty} \le r \vert F-G\vert _{\infty}$, then B is a contraction mapping.
Contraction Properties: if B is a contraction mapping,
- $F^* = BF^*$ has a solution and it is unique
- $F_t = BF_{t-1}$ => $F_t$ -> $F^*$ (value iteration converges)
Bellman operator contracts:
- $BQ(s,a) = R(s,a) + \gamma \sum_{s’}T(s,a,s’) \max_{a’}Q(s’,a’)$
- Given $Q_1, Q_2$, $\left\lVert BQ_1-BQ_2 \right\rVert_{\infty} $ = $\max_{a,s} \Vert \gamma \sum_{s’}T(s,a,s’)(\max_{a’}Q_1(s’,a’)-\max_{a’}Q_2(s’,a’))\Vert $ $\le \gamma \max_{s’} \Vert \max_{a’}Q_1(s’,a’)-\max_{a’}Q_2(s’,a’) \Vert$ $ \le \gamma \max_{s’,a’} \vert Q_1(s’,a’)-Q_2(s’,a’) \vert =\gamma \left \lVert Q_1-Q_2 \right \rVert _{\infty}$
Why might we want to change the reward function for a MDP?
- Easier to solve/represent and similar to what it would have learned
- Because we don’t have one yet
How can we change the MDP reward function without changing the optimal policy?
- multiply by positive constant
- shift by constant (add)
- nonlinear potential-based
18. Game theory
In a 2-player, zero-sum deterministic game of pefect information, minmax=maxmin and there always exists an optimal pure strategy for each player.
Nash Equilibrium: n players with strategies $s_1, s_2, \ldots, s_n$, $s_1^* \in s_1, s_2^* \in s_2, \ldots, s_n^* \in s_n$ are a Nash Equilibrium if and only if $\forall i, s_i^{*} = argmax_{s_i} utility(s_1^{*}, \ldots, s_i, \ldots, s_n^{*})$.
- In the n-player pure strategy game, if elimination of all strictly nominated strategies, eliminates all but one combination of strategies, then that combination is in fact the unique Nash equilibrium.
- Any Nash equilibrium will survive the iterated elimination of strictly dominated strategies. In other words if you get rid of things that are strictly dominated you will not accidentally get rid of nash equilibria in the process.
- If n is finite, that is you have a finite number of players, and for each of the set of strategies, that set of strategies is also finite, in other words you’re still in a finite game, then there exists at least one Nash equilibrium which might involve mixed strategies.
In game theory, Folk Theorm refers to a particular result: describes the set of payoffs that can result from Nash strategies in repeated games.
Folk Theorem: any feasible payoff profile that strictly dominates the minmax/security lelve profile can be realized as a Nash equilibrium payoff profile with sufficiently large discount factor.
Stochastic Games:
- S: states
- $A_i$: actions for player i
- T: transitions
- $R_i$: rewards for player i
- $\gamma$: discount




